Data Science and Computing with Python for Pilots and Flight Test Engineers → Classifier Comparison Example

Classifier Comparison Example

A beautiful classifier comparison example from the scikit-learn machine learning library documentation is presented below, reproduced in unabridged form. The code is licensed under BSD 3 Clause License. Make sure to include this notice and link with any redistribution.

A Classification Problem

In the code below, three different data sets are given, corresponding to the three first plots on the left of each row (see code output below). Each datasets consist of red and blue points. The goal of a classifier is to determine the regions, which are to be treated as red or blue, based on the given distribution of data points. The purpose of these regions is to predict, if we are given a new data point, whether this data point will be red or blue (with some probability).

.What makes this problem challenging is:

The boundaries between data points of different color are not straight and can be rather convoluted. A suitable classifier will have the ability to produce region contours of sufficient complexity (you can see that some clearly struggle with some of the datasets).
The data points may not be entirely separated, i.e. there can be red outliers surrounded by blue points and conversely some blue outliers in predominantly red parts.

Classifiers need to decide, how to deal with those outliers and how to draw boundaries between regions (e.g. which data points are representative of a region, which ones are clearly outliers to be ignored or taken into account only partially, and which ones are genuine enclaves of one region in another and deserve to obtain its separate isolating boundary). The goal is to fit the region boundaries well to the data to represent the spirit of the dataset, without overfitting based on every single data point. Some of the classifiers have parameter values that can be set by the user to adjust these decisions.

This, of course, requires some knowledge of the classifier and the effect of its parameters, in addition to knowing which classifier to choose for a particular problem in the first place. In the examples below, many different classifiers are explored and their parameters have already been set for your suitably. After getting the example below to work on your computer, we therefore recommend you create your own random data sets with intermingling red and blue points, and try to find a classifier and suitable parameters, which divides your data sets into suitable regions. You can also try classification of data sets with more than two categories.

Remarks

We are definitively venturing into machine learning techniques here, for instance with the support vector machine (SVM) classifier. We see that the Gaussian process classifier, based on similar mathematics/statistics as the Gaussian process interpolator we introduced in a previous lesson, yields some of the best results.

.The example below shows the power of some of the freely available Python modules, such as the machine learning library scikit-learn. The library is built on the NumPy, SciPy, and Matplotlib libraries, which we have encountered in previous lessons many times before, and it is open source and commercially usable. With this library, and very few lines of code, one can use a variety of classifiers (not that the code below would be even simpler, if only one classifier was used, rather than so many of them).

Note that the code below works only with newer versions of scikit-learn. If you get an error that a function (e.g. DecisionDisplayBoundary is not found in sklearn.inspection), update your version of scikit-learn or modify the code to work with your older version.

# Code source: Gaël Varoquaux
#              Andreas Müller
# Modified for documentation by Jaques Grobler
# License: BSD 3 clause

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.colors import ListedColormap

from sklearn.datasets import make_circles, make_classification, make_moons
from sklearn.discriminant_analysis import QuadraticDiscriminantAnalysis
from sklearn.ensemble import AdaBoostClassifier, RandomForestClassifier
from sklearn.gaussian_process import GaussianProcessClassifier
from sklearn.gaussian_process.kernels import RBF
from sklearn.inspection import DecisionBoundaryDisplay
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import GaussianNB
from sklearn.neighbors import KNeighborsClassifier
from sklearn.neural_network import MLPClassifier
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVC
from sklearn.tree import DecisionTreeClassifier

names = [
    "Nearest Neighbors",
    "Linear SVM",
    "RBF SVM",
    "Gaussian Process",
    "Decision Tree",
    "Random Forest",
    "Neural Net",
    "AdaBoost",
    "Naive Bayes",
    "QDA",
]

classifiers = [
    KNeighborsClassifier(3),
    SVC(kernel="linear", C=0.025, random_state=42),
    SVC(gamma=2, C=1, random_state=42),
    GaussianProcessClassifier(1.0 * RBF(1.0), random_state=42),
    DecisionTreeClassifier(max_depth=5, random_state=42),
    RandomForestClassifier(
        max_depth=5, n_estimators=10, max_features=1, random_state=42
    ),
    MLPClassifier(alpha=1, max_iter=1000, random_state=42),
    AdaBoostClassifier(random_state=42),
    GaussianNB(),
    QuadraticDiscriminantAnalysis(),
]

X, y = make_classification(
    n_features=2, n_redundant=0, n_informative=2, random_state=1, n_clusters_per_class=1
)
rng = np.random.RandomState(2)
X += 2 * rng.uniform(size=X.shape)
linearly_separable = (X, y)

datasets = [
    make_moons(noise=0.3, random_state=0),
    make_circles(noise=0.2, factor=0.5, random_state=1),
    linearly_separable,
]

figure = plt.figure(figsize=(27, 9))
i = 1
# iterate over datasets
for ds_cnt, ds in enumerate(datasets):
    # preprocess dataset, split into training and test part
    X, y = ds
    X_train, X_test, y_train, y_test = train_test_split(
        X, y, test_size=0.4, random_state=42
    )

    x_min, x_max = X[:, 0].min() - 0.5, X[:, 0].max() + 0.5
    y_min, y_max = X[:, 1].min() - 0.5, X[:, 1].max() + 0.5

    # just plot the dataset first
    cm = plt.cm.RdBu
    cm_bright = ListedColormap(["#FF0000", "#0000FF"])
    ax = plt.subplot(len(datasets), len(classifiers) + 1, i)
    if ds_cnt == 0:
        ax.set_title("Input data")
    # Plot the training points
    ax.scatter(X_train[:, 0], X_train[:, 1], c=y_train, cmap=cm_bright, edgecolors="k")
    # Plot the testing points
    ax.scatter(
        X_test[:, 0], X_test[:, 1], c=y_test, cmap=cm_bright, alpha=0.6, edgecolors="k"
    )
    ax.set_xlim(x_min, x_max)
    ax.set_ylim(y_min, y_max)
    ax.set_xticks(())
    ax.set_yticks(())
    i += 1

    # iterate over classifiers
    for name, clf in zip(names, classifiers):
        ax = plt.subplot(len(datasets), len(classifiers) + 1, i)

        clf = make_pipeline(StandardScaler(), clf)
        clf.fit(X_train, y_train)
        score = clf.score(X_test, y_test)
        DecisionBoundaryDisplay.from_estimator(
            clf, X, cmap=cm, alpha=0.8, ax=ax, eps=0.5
        )

        # Plot the training points
        ax.scatter(
            X_train[:, 0], X_train[:, 1], c=y_train, cmap=cm_bright, edgecolors="k"
        )
        # Plot the testing points
        ax.scatter(
            X_test[:, 0],
            X_test[:, 1],
            c=y_test,
            cmap=cm_bright,
            edgecolors="k",
            alpha=0.6,
        )

        ax.set_xlim(x_min, x_max)
        ax.set_ylim(y_min, y_max)
        ax.set_xticks(())
        ax.set_yticks(())
        if ds_cnt == 0:
            ax.set_title(name)
        ax.text(
            x_max - 0.3,
            y_min + 0.3,
            ("%.2f" % score).lstrip("0"),
            size=15,
            horizontalalignment="right",
        )
        i += 1

plt.tight_layout()
plt.show()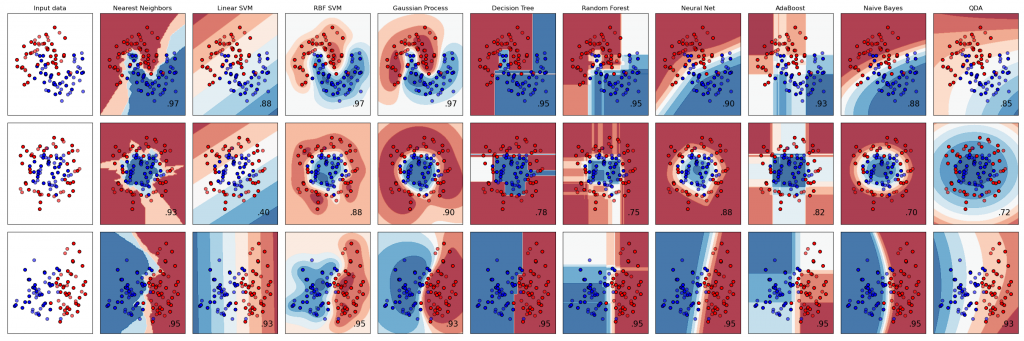

scikit-learn classifier comparison example by Gaël Varoquaux and Andreas Müller.

Clearly, as a student, you now see and know how to write code to use these classifiers. But you do not know yet, how they work, what the advantages and disadvantages are, how to set their parameters for individual problems, and perhaps how to modify them to fit your needs. We therefore encourage you to explore machine learning literature and the internet and learn more about these classifiers and about machine learning in general.

Example Application of Classification

Why do we care about classification, as illustrated above? To illustrate its utility with an example, imagine you show images of faces of cats and dogs to a computer, and you program the computer to extract some features from the images (this could be color, histogram of gradients, etc.), but for the purpose of simplicity, let us say that the computer manages to extract ear length and eye distance by some means. This procedure now assigns for each cat or dog image a data point in a two dimensional feature parameter space, just as in the example above.

For instance, on the horizontal axis could be the ear length and on the vertical axis could be the eye distance. Red data points could be from images of cats, and blue points could be from images of dogs. If these data points are reasonably separated into distinct regions, this now provides a means for the computer to distinguish between cat and dog images, provided you find a way to draw these regions based on the existing data. Drawing these regions is what we do in this problem, and it is the part where the machine is learning based on an existing training data set with known results, how to perform the cat and dog classification.

Your eventual goal is for the computer to predict for an unknown image, if it is a cat or a dog. For an unknown image, you let the computer again measure ear length and eye distance (by some means not discussed here), and you get a new data point somewhere in this two-dimensional feature space. If this data point lies in the red region, the computer shall predict (with some probability) that it is a cat, and if the image lies in the blue region, the computer will predict that it is a dog.

In order to achieve this classification into cats and dogs reliably, you need a good initial training data set, you need to choose a good set of features to be extracted, and you need to draw the region boundaries with a classifier very well (as detailed as possible, but in particular also without overfitting). Of course, the computer will make errors sometimes in its predictions, if the data sets are not entirely disjoint and outliers in the other region are present. Nevertheless, the goal is to draw these regions such that you get the best possible cat and dog classification. (You may want to use a validation data set in this optimization effort, not only a training data set, or your final solution is likely to overfit.)

In this lesson, we concerned ourselves only with the region drawing aspect in this example, and assumed the red and blue data points as already given. The feature extraction from images in the cat and dog illustration (i.e. how the computer determines ear length and eye distance of the animals – and whether these are desirable features to be extracted in the first place) is beyond the scope of this lesson. You could even let the computer decide on its own, which features to extract from an image, e.g. by using a convolutional neural network. Of course, if you do so, you also likely lose insights into how the computer does the classification, and you may miss the fact that ear length and eye distance correlation provides a powerful distinction between the two animals. Your classifier then becomes a black box, albeit perhaps one which works even better. This then takes us into the realm of deep learning.

Machine learning, computer vision, and artificial intelligence, are all subjects we encourage you to explore further. Contact us to receive further guidance and instruction for your quest.